Filtering Signal With Low and High Pass Filter

clear all;
close all;
Fc=100;
Fc2=300;
Fs=1000;
n1=5;
n2=25;
Wn=2*Fc/Fs;
Wn2=2*Fc2/Fs;
f=linspace(-Fs/2,Fs/2,1024);%frequency domain.

[b,a]=butter(n1,Wn,'low');

%butter function is used
% to create filter coefficients.

[c,d]=butter(n2,Wn,'low');
% in third column of
%butter function we decide whether it is low pass filter
% or high pass filter

[y,u]=butter(n1,Wn2,'high');
[x,z]=butter(n2,Wn2,'high');
   
   %LOW PASS FILTERS

[h,w]=freqz(b,a);
h=freqz(b,a,1024);

%with freqz function we obtain the frequency response
%of our filter.

[h1,w1]=freqz(c,d);
h1=freqz(c,d,1024);

        %HIGH PASS FILTERS

[h2,w2]=freqz(y,u);
h2=freqz(y,u,w2);

[h3,w3]=freqz(x,z);
h3=freqz(x,z,w3);


plot(abs(h));
hold on;

plot(abs(h1));
hold on;

plot(abs(h2));
hold on;

plot(abs(h3));
legend('LP order 5','LP order 25','HP order 5','HP order 25');

%           APPLYING THE FILTER TO A SIGNAL

t=0:1/Fs:0.5;
sig=cos(2*pi*50*t)+sin(2*pi*75*t)+cos(2*pi*120*t)+sin(2*pi*385*t);

y1=filter(c,d,sig);
%In time domain filter function
% takes two inputs which are filter coefficient(c and d)
%vectors and it takes the signal which is wanted to filter.
y2=filter(x,z,sig);
figure(2);
y1=fft(y1,1024);
% after filtering we can use fft function
%to obtain our signal in frequency domain.


%           PLOTTING
subplot(3,1,1);
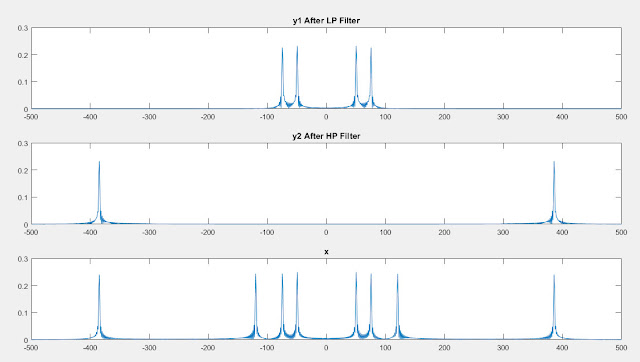
plot(f,fftshift(abs(y1))/1024);
title('y1 After LP Filter');
y2=fft(y2,1024);
subplot(3,1,2);
plot(f,fftshift(abs(y2))/1024);
title('y2 After HP Filter');
sig=fft(sig,1024);
subplot(3,1,3);
plot(f,fftshift(abs(sig))/1024);
title('x');